AVL 트리(AVL Tree) & 트립(Treap)

AVL Tree

개념

위키트리

​ AVL 트리는 각각의 노드(node, 분기점)마다 왼쪽과 오른쪽 부분 트리(sub-tree)의 높이 차이에 대한 정보를 가지며 부분 트리의 높이 차이가 1보다 크지 않은 성질을 가진다. 균형 잡힌 AVL 트리는 n개의 원소가 있을 때 O(log n)의 시간복잡도로 검색, 삽입, 삭제를 할 수 있다. 그러나 삽입과 삭제를 할 때에는 원하는 노드를 찾기 위해 2개의 경로가 필요하기 때문에 레드-블랙 트리만큼 효율이 좋지 않아 자주 쓰이지는 않는다.

​ AVL 트리의 핵심 개념 가운데 하나가 높이 균형 성질(Height-Balance Property)이다. 높이 균형 성질은 자식 노드들의 높이 차이를 뜻한다. 두 서브트리의 높이가 같거나 leaf 노드이면 BF는 0이다. (empty tree의 BF는 -1로 정의한다)

​ AVL 트리의 조건을 만족하는 트리가 n개의 원소를 갖는다고 할때, 높이는 logn이라는 사실을 알 수 있다. 또한, 이진 탐색 트리에서의 검색 시간복잡도는 트리의 높이이므로 AVL 트리의 검색 시간 또한 O(logn)임을 알수있다.

​

동작

• 삽입
  • AVL 트리 T에 노드 d를 삽입하기 위해 T에서 d가 단말 노드(leaf node)로 삽입될 수 있도록 하는 노드 w를 찾고, w의 자식으로 d를 삽입한다.
  • d를 삽입했을때 트리가 불균형해지면 세 노드를 기준으로 회전(rotation)을 시킴으로써 균형을 맞춘다.
• 회전/삭제
  • 해당 블로그 참조

​

계산복잡성

• 삽입 : O(logn)
• 삭제 : O(logn)

​

​

Treap

개념

​ 트립은 트리(tree)와 힙(heap)의 합성어이다. 트립은 각 노드가 값 이외의 별도의 우선순위(priority)를 가지고 있다. 트립은 값의 측면에서는 이진검색트리의 특성(왼쪽 트리는 자신보다 작은 값들, 오른쪽 트리는 자신보다 큰 값들)을 가지지만, 우선순위는 힙의 특성(부모의 우선순위는 자식의 우선순위보다 높다)를 유지하게 된다.

​ 이 우선순위 값은 입력 순서에 상관없이 랜덤한 값으로 주어진다. 이렇게 만들어진 트립은 우선순위 순서대로 값을 넣은 이진 탐색 트리와 동일하게 된다. 즉, 값의 입력 순서를 랜덤하게 해준 이진 탐색 트리라 볼 수 있다. 따라서 운이 안 좋으면 치우쳐진 트리를 얻을 수도 있겠지만, 그러한 가능성은 현저히 낮다.

​

Introduction To Algorithm 번역

​ 이진 검색 트리에 n개의 항목 집합을 삽입하면 결과 트리가 끔찍하게 불균형해 검색 시간이 길어질 수 있다. 따라서 평균적으로 고정된 항목 세트에 대해 균형 잡힌 트리를 구축하는 한 가지 전략은 항목을 무작위로 치환한 다음 해당 순서대로 트리에 삽입하는 것이다.

​ 한 번에 모든 항목이 없으면 어떻게할까? 항목을 한 번에 하나씩 받으면 여전히 무작위로 이진 검색 트리를 만들 수 있나? 이 질문에 긍정적으로 답하는 데이터 구조를 살펴보겠다.

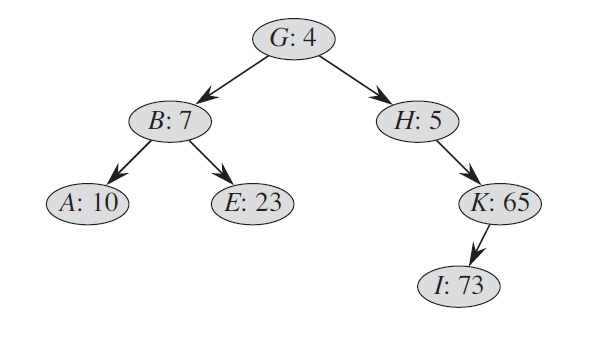
​ Treap은 노드 정렬 방식이 수정된 이진 검색 트리이다. 위 그림은 예를 보여준다. 평소와 같이 트리의 각 노드 x에는 키값 x가 있다. 또한, 각 노드에 대해 독립적으로 선택된 난수인 x의 우선순위 값을 할당한다. 우리는 모든 우선순위가 구별되고 모든 키가 구별된다고 가정한다. Treap의 노드는 키가 Binary Search Tree 속성을 따르고, 우선순위가 Min Heap Order 속성을 따르도록 정렬된다.

1. Value가 u의 왼쪽 자식이면 Value.key < u.key
2. Value가 u의 오른쪽 자식이면 Value.key > u.key
3. Value가 u의 자식이면 Value.priority > u.priority

​ 이 속성 조합이 Tree를 “Treap”이라고 부르는 이유이다. 이진 검색 트리와 힙의 기능을 모두 가지고 있다. 다음과 같은 방식으로 Treap을 생각하는 것이 도움이 된다. 노드 x1, x2, … xn을 삽입한다고 가정한다. 그런 다음 결과적인 Treap은 노드가 (무작위로 선택한) 우선순위에 따라 지정된 순서대로 일반 이진 검색 트리에 삽입된 경우 형성되었을 트리이다. 즉, xi.priority < xj.priority (i < j)일 것이라는 말이다.

1. 연관된 키와 우선순위가 있는 노드 x1, x2, …, xn 세트가 주어졌을때 모두 구별되며 , 이러한 노드와 연관된 Treap이 고유하다는 것을 보여준다.
2. Treap의 예상 높이가 logn이므로 Treap에서 값을 검색하는데 예상되는 시간이 O(logn)임을 보여준다.

​ 기존 Treap에 새 노드를 삽입하는 방법을 살펴보자. 가장 먼저 할 일은 새 노드에 임의의 우선순위를 할당하는 것이다. 그런 다음 삽입 알고리즘을 호출한다. 이를 TREAP-INSERT라고 한다. 다음 그림을 참고하자.

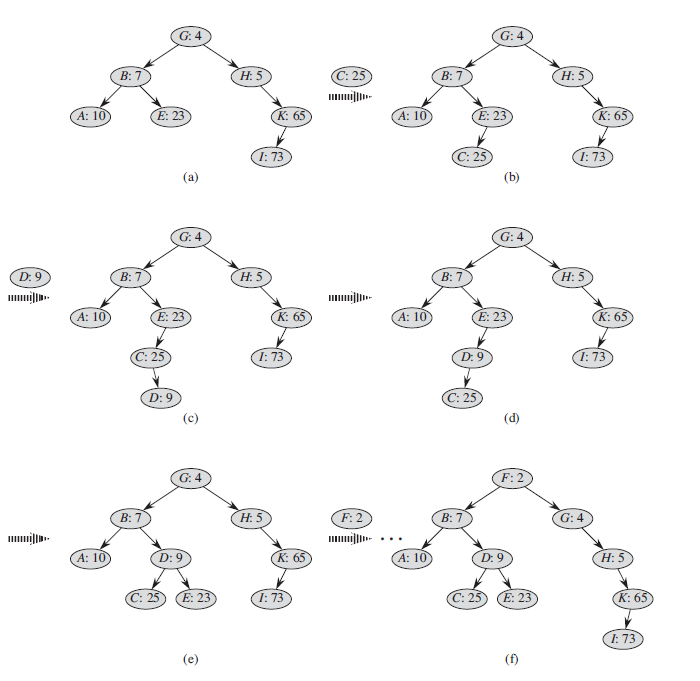
(a) : 삽입 전 TREAP

(b) : 키 C와 우선순위 25를 가진 노드를 삽입한 후 TREAP

(c)-(d) : 키 D와 우선순위 9인 노드를 삽입할때의 과정

(e) : (c) 및 (d) 과정이 완료된 TREAP

(f) : 키 F와 우선순위 2를 가진 노드를 삽입한 후의 TREAP

​ TREAP-INSERT는 검색을 수행한 다음 일련의 회전을 수행한다. 이 두 작업의 예상 실행 시간은 동일하지만 실제로는 비용이 다르다. 검색은 수정하지 않고 Treap에서 정보를 읽는다. 반대로 회전은 TREAP 내에서 부모 및 자식 포인터를 변경한다. 대부분의 컴퓨터에서 읽기 작업은 쓰기 작업보다 훨씬 빠르다. 따라서 TREAP-INSERT가 약간의 회전을 수행하기를 원한다. 수행되는 예상 회전수가 상수에 의해 제한됨을 보여준다.

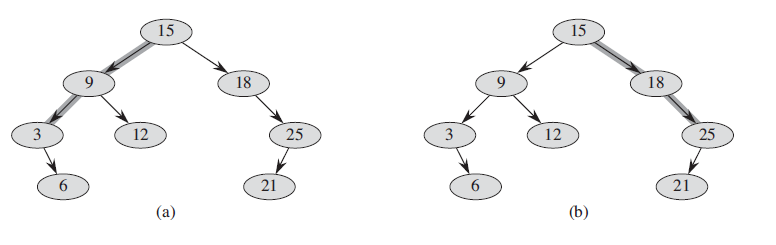
​ 그러기 위해서는 위 그림에 나와있는 몇 가지 정의가 필요하다. 이진 검색 트리 T의 왼쪽 경로는 루트에서 가장 작은 키가 있는 노드까지의 단순 경로이다. 즉, 왼쪽 경로는 왼쪽 가장자리로만 구성된 루트의 단순 경로이다. 대칭적으로 T의 오른쪽 경로는 오른쪽 가장자리로만 구성된 루트의 단순 경로이다.