Red-Black Tree & Interval Tree

Augmenting Data Structure

1. Augmenting Data Structures

​ doubly linked list, hash table, binary search tree와 같은 일부 엔지니어링 상황에는 “교과서” 데이터 구조만 필요하지만, 다른 많은 경우에는 창의력이 필요하다. 하지만 드문 경우에만 완전히 새로운 유형의 데이터 구조를 생성해야 한다. 더 자주, 추가 정보를 저장해 교과서 데이터 구조를 보강하는 것으로 충분하다. 그런 다음 원하는 응용 프로그램을 지원하도록 데이터 구조에 대한 새 작업을 프로그래미 할 수 있다. 그러나 데이터 구조에 대한 일반적인 작업을 통해 추가된 정보를 업데이트하고 유지 관리해야하기 때문에 데이터 구조를 확장하는 것이 항상 간단한 것은 아니다.

​ 이 장에서는 Red-Black Tree로부터 생성하는 두 가지 데이터 구조에 대해 설명한다. 14.1에서는 동적 집합에 대한 일반적인 순서 통계 연산을 지원하는 데이터 구조를 설명할 것이다. 그런 다음 집합에서 i번째로 작은 숫자 또는 집합의 전체 순서에서 주어진 요소의 순위를 빠르게 찾을 수 있다. 14.2에서는 데이터 구조를 보강하는 과정을 추상화하고, Red-Black Tree를 보강하는 과정을 단순히 할 수 있는 정리를 제공한다. 14.3에서는 정리를 사용해 시간 간격과 같은 동적 간격 세트를 유지하기 위한 데이터 구조를 설계하는데 도움을 준다. 쿼리 간격이 주어지면 세트에서 겹치는 간격을 빠르게 찾을 수 있다.

​

14.1 Dynamic order statistics

​ 9장에서는 order statistic의 개념을 소개했다. 특히 n개 요소 집합의 i번째 순서 통계에 관해서 소개했다(i가 {1, 2, …, n} 집합에서 가장 작은 요소). 순서가 지정되지 않은 세트에서 O(n) 시간에 order statistic을 결정하는 방법을 보았다. 이 섹션에서는 O(logn)시간에 동적 집합에 대한 순서 통계를 결정할 수 있도록 Red-Black 트리를 수정하는 방법을 살펴보자. 또한, O(logn)시간에서 요소의 순위(집합의 선형 순서에서의 위치)를 계산하는 방법을 살펴볼 것이다.

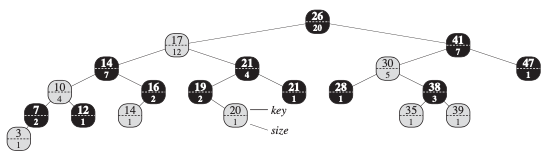
Figure 14.1 확장된 Red-Black Tree (order-statistic tree). 음영 처리된 노드는 빨간색이고, 어두운 노드는 검은색이다. 일반적인 속성 외에도 각 노드 x에는 x에 뿌리를 둔 서브 트리에서 sentinel이 아닌 노드의 number인 x, size가 있다.

​ 그림 14.1은 빠른 order statistic 작업을 지원할 수 있는 데이터 구조를 봉준다. order statistic tree T는 단순히 각 노드에 추가 정보가 저장되어있는 Red-Black Tree이다. 노드 x의 일반적인 Red-Black Tree 속성 x.key, x.color, x.parent, x.left, x.right 외에도 다른 속성인 x.size가 있다. 이 속성은 x, 즉 하위 트리의 크기에 뿌리를 둔 하위 트리의 노드 수를 포함한다. sentinel의 크기를 0으로 정의하면 (즉, T.nil.size를 0으로 설정하면)

x.size = x.elft.size + s.right.size + 1

​ order statistic tree에서는 키르 구별할 필요가 없다(예를 들어, 그림 14.1의 트리에는 값이 14인 키 2개와 값이 21인 키 2개가 있다). 동일한 키가 있는 경우 위의 순위 개념이 잘 정의되어 있지 않다. 우리는 order statistic tree에 대한 이 모호성을 제거하기 위해 요소의 순위를 트리의 순서가 없는 walk에서 print될 위치로 정의한다. 예를 들어 그림 14.1에서 검은색 노드에 저장된 키 14는 랭크 5이고, 빨간색 노드에 저장된 키 14는 랭크 6이다.

​

Retrieving an element with a given ran

​ 삽입 및 삭제 중에 크기 정보를 유지하는 방법을 보여주기 전에, 추가 정보를 사용하는 두 가지 order stastics 쿼리의 구현을 살펴보자. 주어진 순위의 요소를 검색하는 작업으로 시작한다. procedure OS-SELECT(x, i)는 x에 뿌리를 둔 서브 트리에서 i번째로 작은 키를 포함하는 노드에 대한 포인터를 반환한다. order stastics Tree T에서 i번째 작은 키를 가진 노드를 찾기 위해 OS-SELECT(T.root, i)를 호출한다.

node OS-SELECT(x, i)
{
	r = x.left.size + 1
	if i == r
		return x
	elseif i < r
		return OS-SELECT(x.left, i)
	else
		return OS-SELECT(x.right, i - r)
}

​ OS-SELECT의 라인 1에서 우리는 x를 루트로 하는 서브 트리 내의 노드 x의 rank인 r을 계산한다. x.left.size의 값은 x에 뿌리를 둔 서브 트리의 inorder tree walk에서 x앞에 오는 노드의 수이다. 따라서 x.left.size + 1은 x에 뿌리를 둔 하위 트리 내에서 x의 rank이다. i = r이면 노드 x가 i번째 가장 작은 요소이므로 3번 줄에 x를 반환한다. i < r 이면 i번째 가장 작은 요소가 x의 왼쪽 하위 트리에 있으므로 5번 줄의 x.left에서 재귀한다. i > r 이면 i번째 가장 작은 요소가 x의 오른쪽 하위 트리에 있다. x에 뿌리를 둔 하위 트리에는 inorder tree walk에서 x의 오른쪽 하위 트리 앞에 오는 r개의 요소가 포함되어 있으므로 x에 뿌리를 둔 하위 트리에서 i번째로 작은 요소는 x.right에 뿌리를 둔 하위 트리에서 (i - r)번째로 작은 요소이다. 6행은 이 요소를 재귀적으로 들어간다.

​ OS-SELECT의 작동 방식을 보려면 그림 14.1의 order stastics tree에서 17번째로 작은 요소를 검색해보자. 우리는 키가 26이고 i = 17인 루트를 x로 시작한다. 26의 왼쪽 하위 트리의 크기는 12이므로 rank는 13이다. 따라서 rank가 17인 노드는 26의 오른쪽 하위 트리에서 17-13 = 4번째로 작은 요소임을 알 수 있다. 재귀 호출 후 x는, 키는 41이고, i = 4인 노드이다. 41의 왼쪽 하위 트리의 크기가 5이므로 하위 트리 내의 rank는 6이다. 따라서 rank가 4인 노드는 41의 왼쪽 하위 트리에서 네번째로 작은 요소이다. 따라서 다시 한 번 반복해 키 38이 있는 노드에 뿌리를 둔 하위 트리에서 4 - 2 = 2번째로 작은 요소를 찾는다. 이제 왼쪽 하위 트리의 크기가 1로, 두 번째로 작은 요소임을 알 수 있다. 따라서 procedure는 키 38을 사용하는 노드에 대한 포인터를 반환한다.

​ 각 재귀 호출은 order stastics tree에서 한 수준 아래로 내려가기 때문에 OS-SELECT의 총 시간은 트리 높이에 가장 비례한다. tree는 Red-Black Tree이므로 높이는 logn 여기서 n은 노드 수이다. 따라서 OS-SELECT의 실행 시간은 n에 대해 O(log n)이다.

​

Determining the rank of an element

​ order stastics tree T의 노드 X에 대한 포인터가 주어지면 OS-RANK procedure는 T의 inorder tree walk에 의해 결정된 선형 순서로 x의 위치를 반환한다.

int OS-RANK(T, x)
{
	r = x.left.size + 1
	y = x
	while y != T.root
		if y == y.p.right
			r = r + y.p.left.size + 1
		y = y.p
	return r
}

​ prodcedure는 다음과 같이 작동한다. 노드 x의 순위는 inorder tree walk에서 x앞에 오는 노드의 수에 x자체에 1을 더한 것으로 생각할 수 있다. OS-RANK는 다음 루프를 불변으로 유지한다:

3~6행의 while 루프가 반복될때마다 r은 노드 y에 뿌리를 둔 하위 트리에서 x.key의 rank이다.

이 루프를 사용해 OS-RANK가 다음과 같이 올바르게 동작함을 보여준다.

Initialization: 첫 번째 반복 이전에 1번 줄은 r을 x에 뿌리를 둔 하위 트래 내 x.key의 rank로 설정한다. line 2에서 y = x를 설정하면 라인 3의 테스트가 처음 실행될 때 불변성이 참이 된다.

Maintenance: while 루프의 각 반복이 끝날 때 y = y.p를 설정한다. 따라서 r이 루프 본문의 시작 부분에서 y에 뿌리를 둔 하위 트리의 x.key rank인 경우, r은 루프 본문의 끝에서 y.p를 루트로 하는 하위 트리의 x.key rank이다. while 루프를 반복할 때마다 y.p에 뿌리를 둔 하위 트리를 고려한다. 우리는 이미 inorder walk에서 x앞에 오는 노드 y에 뿌리를 둔 하위 트리의 노드 수를 계산했으므로 inorder walk에서 x앞에 오는 y의 형제에 뿌리를 둔 하위 트리에 노드를 축하고, y에 1을 더해야한다. 그것도 x앞에 온다. y가 왼쪽 자식이면 y.p 또는 y.p의 오른쪽 하위 트리에 있는 노드가 x앞에 나오지 않으므로 r은 그대로 둔다. 그렇지 않으면 y는 오른쪽 자식이고, y.p 자체와 마찬가지로 y.p의 왼쪽 하위 트리에 있는 모든 노드가 x앞에 있다. 따라서 5행에서 r의 현재 값에 y.p.left.size + 1을 추가한다.

Termination: 루프는 y = T.root 일 때 종료되므로 y에 뿌리를 둔 하위 트리가 전체 트리가 된다. 따라서 r의 값은 전체 트리에서 x.key의 순위이다.

​ 예를 들어 그림 14.1의 order stastics tree에서 OS-RANK를 실행해 38번 키가 있는 노드의 순위를 찾을 때 while 루프의 맨 위에 있는 y.key 및 r값의 다음 시퀀스를 얻는다:

iteration	y.key		r
	1		38			2
	2		30			4
	3		41			4
	4		26			17

procedure는 17 rank를 반환한다.

​ while 루프의 각 반복은 O(1) 시간이 걸리고, y는 반복할 때마다 트리에서 한 수준 위로 올라가므로 OS-RANK의 실행 시간은 트리 높이에 가장 비례한다: n개의 노드를 가지는 order stastics tree 에서 O(log n)

​

Maintaining subtree sizes

​ 각 노드의 size attribute가 주어지면 OS-SELECT 및 OS-RANK는 order stastics 정보를 빠르게 계산할 수 있다. 그러나 우리가 Red-Black Tree에 대한 기본 수정 작업 내에서 이러한 속성을 효율적으로 유지할 수 없다면 우리의 작업은 소용이 없을 것이다. 이제 두 작업의 점근적 실행 시간에 영향을 주지 않고, 삽입-삭제 모두에 대한 하위 트리 크기를 유지하는 방법을 보여줄 것이다.

​ 13.3 절에서 Red-Black Tree에 삽입하는 것은 두 단계로 구성된다는 점에 주목했다. 첫 번째 단계는 루트에서 트리 아래로 내려가 새 노드를 기존 노드의 자식으로 삽입한다. 두 번째 단계는 트리 위로 올라가 색상을 변경하고 회전을 수행해 Red-Black 속성을 유지한다.

​ 첫 번째 단계에서 하위 트리 크기를 유지하기 위해 루트에서 leaf로 이동하는 단순 경로에서 각 노드 x에 대해 x.size를 증가시킨다. 추가된 새 노드의 크기는 1이 된다. 순회 경로에 log n개의 노드가 있으므로 크기 속성을 유지하는 추가 비용은 O(log n)이다.

​ 두 번째 단계에서 기본 Red-Black Tree의 유일한 구조적 변경은 회전에 의해 발생하며, 그 중 최대 2개가 있다. 또한, 회전은 로컬 작업이다: 두 개의 노드만 크기 속성이 무효화된다. 회전이 수행되는 링크는 이 두 노드에서 발생한다. 섹션 13.2의 LEFT-ROTATE(T, X)에 대한 코드를 참조해 다음 줄을 추가한다.

y.size = x.size
x.size = x.left.size + x.right.size + 1

Figure 14.2 회전 중 하위 트리 크기 업데이트. 우리가 회전하는 링크는 크기 속성을 업데이트 해야하는 두 노드에서 발생한다. 업데이트는 로컬이므로 x, y에 저장된 크기 정보와 삼각형으로 표시된 하위 트리의 루트만 필요하다.

​ 그림 14.2는 속성이 업데이트되는 방법을 보여준다. RIGHT-ROTATE로의 변경은 대칭이다.

​ Red-Black Tree에 삽입하는 동안 최대 두 번의 회전이 수행되기 때문에 두 번째 단계에서 크기 속성을 업데이트하는데 O(1) 추가 시간만 소비한다. 따라서 n-node order stastics tree에 삽입하는데 걸리는 총 시간은 O(log n)이며, 이는 일반 Red-Black Tree와 점근적으로 동일하다.

​ Red-Black Tree에서의 삭제는 또한 두 단계로 구성된다. 첫 번째 단계는 기본 검색 트리에서 작동하고, 두 번째 단계는 최대 세 번의 회전을 일으키고 그렇지 않으면 구조적 변경을 수행하지 않는다. 첫 번째 단계는 트리에서 노드 y를 제거하거나 트리 내에서 위로 이동한다. 하위 트리 크기를 업데이트하려면 노드 y에서 루트까지 간단한 경로를 탐색해 경로에 있는 각 노드의 크기 속성을 줄인다. 이 경로는 n-node Red-Black Tree에서 log n의 길이를 갖기 때문에 첫 번째 단계에서 크기 속성을 유지하는데 소요되는 추가 시간은 O(log n)이다. 두 번째 삭제 단계에서 삽입과 동일한 방식으로 O(1) 회전을 처리한다. 따라서 크기 속성 유지를 포함해 삽입과 삭제 모두 n-node order stastics Tree에 대해 O(log n)이 걸린다.

​

14.2 How to augment a data structure

​ 추가 기능을 지원하기 위해 기본 데이터 구조를 보강하는 프로세스는 알고리즘 설계에서 매우 자주 발생한다. 간격에 대한 연산을 지원하는 데이터 구조를 설계하기 위해 다음 섹션에서 다시 사용할 것이다. 이 섹션에서는 이러한 증가와 관련된 단계를 살펴본다. 우리는 또한 많은 경우에 Red-Black Tree를 쉽게 증가시킬 수 있는 정리를 증명할 것이다.

​ 데이터 구조를 보강하는 프로세스를 네 단계로 나눌 수 있다:

1. 기본 데이터 구조를 선택한다.
2. 기본 데이터 구조를 유지하기 위한 추가 정보를 결정한다.
3. 기본 데이터 구조에 대한 기본 수정 작업의 추가 정보를 유지 할 수 있는지 확인한다.
4. 새로운 기능을 개발한다.

​ 규정된 설계 방법과 마찬가지로 주어진 순서대로 단계를 맹목적으로 따르지 말아라. 대부분의 설계 작업에는 시행 착오 요소가 포함되어 있으며 모든 단계의 진행은 일반적으로 병렬로 진행된다. 예를 들어, 추가 정보를 효율적으로 유지할 수 없다면 추가 정보를 결정하고 새로운 기능을 개발하는데 (2단계 및 4단계) 의미가 없다. 그럼에도 불구하고 이 4단계 방법은 데이터 구조를 보강하려는 노력에 좋은 초점을 제공하며, 보강된 데이터 구조의 문서를 구성하는 좋은 방법이기도 하다.

​ order stastics tree를 디자인하기 위해 section 14.1에서 이 단계를 따랐다. 1단계에서는 기본 데이터 구조로 Red-Black Tree를 선택했다. Red-Black Tree의 적합성에 대한 단서는 MINIMUM, MAXIMUM, SUCCESSOR, PREDECESSOR와 같은 total order에 대한 다른 동적 집합 작업을 효율적으로 지원하는데 있다.

​ 2단계에서는 각 노드 x가 x에 뿌리를 둔 서브 트리의 크기를 저장하는 size 속성을 추가했다. 일반적으로 추가 정보는 작업을 보다 효율적으로 만든다. 예를 들어, 트리에 저장된 키만 사용해 OS-SELECT 및 OS-RANK를 구현할 수 있지만, O(log n)에 실행되지 않았다.

​ 3단계에서는 삽입 및 삭제가 O(log n)에 계속 실행되는 동안 크기 속성을 유지할 수 있음을 확인했다. 이상적으로는 추가 정보를 유지하기 위해 데이터 구조의 몇 가지 요소만 업데이트하면 된다. 예를 들어, 단순히 각 노드에 해당 순위를 트리에 저장하면 OS-SELECT 및 OS-RANK procedure가 빠르게 실행되지만, 새로운 최소 요소를 삽입하면 트리의 모든 노드에서 이 정보가 변경된다. 대신 서브 트리 크기를 저장할 때 새 요소를 삽입하면 정보가 O(log n)에 변경된다.

​ 4단게에서는 OS-SELECT 및 OS-RANK 기능을 개발했다. 결국 새로운 기능이 필요하기 때문에 처음에 데이터 구조를 강화해야한다. 때때로 새로운 기능을 개발하는 대신 기존 작업을 신속하게 처리하기 위해 추가 정보를 사용한다.

​

14.3 Interval trees

​ 이 섹션에서는 dynamic sets of interval에 대한 작업을 지원하기 위해 Red-Black tree를 augment할 것이다. 닫힌 구간은 t1<=t2 범위의 정렬된 실수 [t1, t2]이다. 구간 [t1, t2]는 집합 {t1 <= t <= t2}를 나타낸다. Open 그리고 half-open interval은 각각 세트에서 끝점 중 하나 또는 둘 모두를 생략한다. 이 섹션에서는 interval이 닫혀 있다고 가정한다. 결과를 open 및 half-open interval로 확장하는 것은 개념적으로 간단하다.

​ Interval은 연속적인 기간을 차지하는 이벤트를 나타내는데 편하다. 예를 들어, 주어진 간격 동안 발생한 이벤트를 찾기 위해 시간 간격의 데이터베이스를 쿼리 할 수 있다. 이 섹션의 데이터 구조는 이러한 간격 데이터베이스를 유지하기 위한 효율적인 방법을 제공한다.

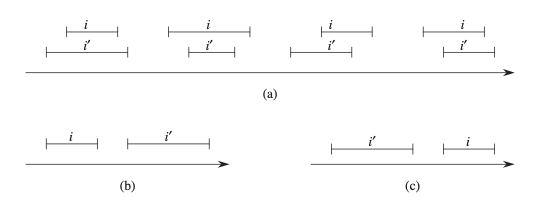
Figure 14.3 두 개의 닫힌 구간 i와 i’에 대한 interval 삼분법. (a) i와 i’가 겹치는 경우 네 가지 상황이 있다; 각각, i.low <= i’.high 및 i’.low <= i.high (b) interval은 겹치지 않는다. i.high < i’.low (c) interval이 겹치지 않는다. i’.high < i.low

​ 우리는 i.low = t1 (the low endpoint) 속성과 i.high = t2 (the high endpoint) 속성을 사용해 구간 [t1, t2]를 객체 i로 나타낸다. 우리는 i.low <= i’.high 와 i’.low <= i.high 조건을 만족하면 구간 i와 i’이 겹친다고 말한다. 그림 14.3에서 볼 수 있듯이 두 구간 i와 i’은 interval 삼분법을 충족한다. 즉, 다음 세 가지 속성 중 정확히 하나가 유지된다.

1. i 와 i’은 겹친다.
2. i는 i’의 왼쪽에 있다. (i.high < i’.low)
3. i는 i’의 오른쪽에 있다. (i’.high < i.low)

​ interval tree는 각 요소 x가 interval x.int를 포함하는 동적 요소 집합을 유지하는 Red-Black Tree이다. Interval Tree는 다음 작업을 지원한다.

1. INTERVAL-INSERT (T, x) : int 속성이 interval을 포함하는 것으로 간주되는 요소 x를 interval tree T에 추가한다.
2. INTERVAL-DELETE (T, x) : 구간 트리 T에서 x 요소를 제거한다.
3. INTERVAL-SEARCH (T, i) : x.int가 interval i와 겹치도록 interval Tree T의 요소 x에 대한 포인터를 반환하거나, 그러한 요소가 세트에 없으면 sentinel T.nil에 대한 포인터를 반환한다.

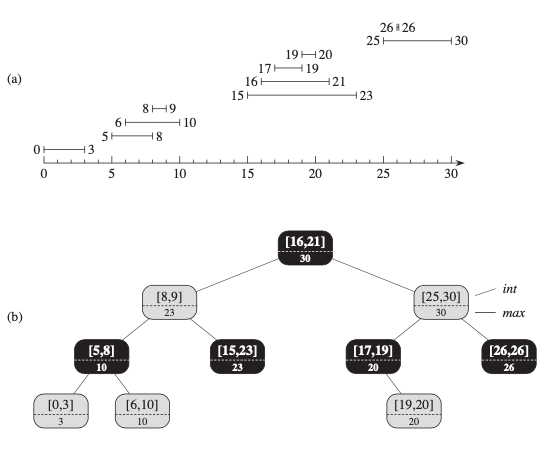
Figure 14.4 Interval Tree. (a) 왼쪽 끝점을 기준으로 아래쪽에서 위쪽으로 정렬된 10개의 interval set (b) 그들을 나타내는 interval tree. 각 노드 x에는 점섬 위에 표시된 interval과 점선 아래에 표시된 x를 루트로 하는 하위 트리에 있는 간격 끝점의 최대값이 포함된다. 트리의 inorder tree walk는 왼쪽 끝점을 기준으로 정렬된 순서로 노드를 나타낸다.

​ 그림 14.4는 interval tree가 interval 집합을 나타내는 방법을 보여준다. interval tree의 디자인과 여기에서 실행되는 작업을 검토 할 때 섹션 14.2의 4단계 방법을 추적할 것이다.

Step 1 : 기본 데이터 구조

​ 우리는 각 노드 x가 interval x.int를 포함하고, x의 키가 interval의 낮은 끝점인 x.int.low인 Red-Black Tree를 선택한다. 따라서 데이터 구조의 inorder tree walk는 하위 end point 별로 정렬된 순서로 간격을 나열한다.

Step 2 : 추가 정보

​ interval 자체 외에도 각 노드 x에는 x를 루트로 하는 하위 트리에 저장된 간격 끝점의 최대값인 x.max 값이 포함된다.

Step 3 : 정보 유지

​ n 노드의 interval tree에서 삽입 및 삭제가 O(log n) 시간이 걸리는지 확인해야한다. x.int interval로 x.max와 노드 x 자식의 최대값을 결정할 수 있다.

x.max = max(x.int.high, x.left.max, x.right.max)

​ 따라서 정리 14.1에 따르면 삽입 및 삭제는 O(log n) 시간으로 실행된다.

Step 4 : 새로운 연산 개발

​ 우리가 필요로 하는 유일한 새로운 연산은 INTERVAL-SEARCH (T, i)로, 트리 T에서 interval이 interval i와 겹치는 노드를 찾는다. 트리에서 i와 겹치는 interval이 없으면 procedure는 sentinel T.nil에 대한 포인터를 반환한다.

node INTERVAL-SEARCH(T, i)
{
	x = T.root
	while x != T.nil && i does not overlap x.int
		if x.left != T.nil and x.left.max >= i.low
			x = x.left
		else x = x.right
	return x
}

​ i와 겹치는 구간에 대한 검색은 tree의 루트에서 x로 시작해 아래쪽으로 진행된다. 겹치는 interval을 찾거나 x가 sentinel T.nil을 가리킬때 종료된다. 기본 루프의 각 반복은 O(1) 시간이 걸리고, n 노드 Red-Black Tree의 높이가 log n이므로 INTERVAL-SEARCH 절차는 O(log n) 시간이 걸린다.

​ INTERVAL-SEARCH가 올바른 이유를 보기 전에 그림 14.4의 interval tree에서 어떻게 작동하는지 살펴보자. 구간 i = [22, 25]와 겹치는 구간을 찾고 싶다고 가정해보자. 우리는 x를 루트로 시작하는데, 이것은 [16, 21]을 포함하고 i와 겹치지 않는다. x.left.max = 23이 i.low = 22 보다 크므로 루프는 루트의 왼쪽 자신인 [8, 9]인 x를 사용한다. 이번에는 x.left.max = 10이 i.low = 22 보다 작으므로 루프는 오른쪽 x로 계속한다. 이 노드에 저장된 구간 [15, 23]이 i와 겹치므로 프로시저는 이 노드를 반환한다.

​ 실패한 검색의 예로서, 그림 14.4의 interval tree에서 i = [11, 14]와 겹치는 interval을 찾고 싶다고 가정하자. 다시 한 번 x를 루트로 시작한다. 루트의 구간 [16, 21]은 i와 겹치지 않고, x.left.max = 23이 i.low = 11 보다 크므로 [8, 9]를 포함하는 노드로 왼쪽으로 이동한다. interval [8, 9]와 i는 겹치지 않고, x.left.max = 10이 i.low = 11 보다 작으므로 오른쪽으로 이동한다. interval [15, 23]은 i와 겹치지 않고 왼쪽 자식은 T.nil이므로 다시 오른쪽으로 이동해 루프를 종료하고 sentinel T.nil을 반환한다.

​ INTERVAL-SEARCH가 올바른 이유를 확인하려면 루트에서 단일 경로를 검사하는 것이 충분한 이유를 이해해야한다. 기본 아이디어는 모든 노드 x에서 x.int가 i와 겹치지 않으면 검색이 항상 안전한 방향으로 진행된다는 것이다. 트리에 겹치는 간격이 있으면 검색이 확실히 겹치는 간격을 찾는다. 다음 정리는 이 속성을 보다 정확하게 설명한다.

​

Theorem 14.3

​ INTERVAL-SEARCH(T, i)를 실행하면 interval이 i와 겹치는 노드를 반환하거나, 트리 T에 간격이 i와 겹치는 노드가 없으면 T.nil을 반환한다.

Proof : 2~5행의 while 루프는 x = T.nil 또는 i가 x.int와 겹칠 때 종료된다. 후자의 경우 x를 반환하는 것이 확실히 옳다. 따라서 우리는 x = T.nil 때문에 while 루프가 종료되는 전자의 경우에 집중한다. 2~5행의 while 루프에 대해 다음은 불변이다.

Tree T에 i와 겹치는 구간이 포함되어 있으면 x에서 루트가 지정된 하위 트에 interval이 포함된다.

이 루프의 불변성은 다음과 같다.

Initialization : 첫 번째 반복 이전에 라인 1은 x를 T의 근으로 설정해 불변성이 유지되도록 한다.

Maintenance : while 루프의 각 반복은 4행 또는 5행을 실행한다. 두 경우 모두 루프가 불변을 유지함을 보여줄 것이다.

​ 3행의 분기 조건에 부합해서 5행이 실행되면 x.left = T.nil 또는 x.left.max < i.low 이다. x.left = T.nil인 경우 x.left에 뿌리를 둔 서브 트리는 i와 겹치는 interval을 분명히 포함하지 않으므로 x를 x.right로 설정하면 불변성이 유지된다. 따라서 x.left != T.nil 및 x.left.max < i.low라고 가정한다. 그림 14.5 (a)에서 알 수 있듯이 x’s 왼쪽 하위 트리에 있는 간격 i’에 대해 다음과 같다.

i'.high <= x.left.max
		< i.low

따라서 interval 삼분법에 의해 i’와 i는 겹치지 않는다. 따라서 x의 왼쪽 하위 트리에는 i와 겹치는 구간이 없으므로 x를 x.right로 설정하면 불변성이 유지된다.

​ 반면에 4행이 실행되면 루프 불변성의 반대가 유지됨을 보여줄 것이다. 즉, x.left에 뿌리를 둔 서브트리가 i와 겹치는 간격을 포함하지 않으면 트리의 어느 곳에서도 i와 겹치는 간격이 없다. 4행이 실행되었으므로 3행의 분기 조건으로 인해 x.left.max >= i.low이다. 또한, max 속성의 정의에 따라 x의 왼쪽 하위 트리에는 다음과 같은 간격 i’이 포함되어야한다.

i'.high =   x.left.max
		>= i.low

(그림 14.5 (b)는 상황을 보여준다.) i와 i’는 겹치지 않고, i’.high < i.low가 사실이 아니기 때문에 i.high < i’.low라는 구간 삼분법에 따른다. Interval 트리는 간격의 낮은 끝점에 키가 지정되므로 검색 트리 속성은 x의 오른쪽 하위 트리에 있는 간격 i’‘에 대해 다음을 의미한다.

i.high	<  i'.low
		<= i''.low

​ 간격 삼분법에 의해 i와 i’‘은 겹치지 않는다. x의 왼쪽 하위 트리의 간격이 i와 겹치는지 여부에 관계없이 x를 x.left로 설정하면 불변성이 유지된다.

Termination : x = T.nil 일때 루프가 종료되면 x에 뿌리를 둔 서브 트리는 i와 겹치는 간격을 포함하지 않는다. 루프 불변성의 반대 양성은 T에 i와 겹치는 구간이 없음을 의미한다. 따라서 x = T.nil을 반환하는 것이 옳다.

​ 따라서 INTERVAL-SEARCH 프로시저가 올바르게 작동한다.