Efficient and easy segment trees

Efficient and easy segment trees

번역 원본 LINK

Segment tree with single element modifications

​ 세그먼트 트리에 대해 간략한 설명부터 시작해보자. 세그먼트 트리는 우리에게 배열이 있고, 연속된 세그먼트들에 대해 약간의 변화와 쿼리 요청이 필요할 때 사용한다. 첫 번째 예시에서 두 가지 작업을 고려한다:

1. modify one elment in the array
2. find the sum of elements on some segment

Perfect binary tree

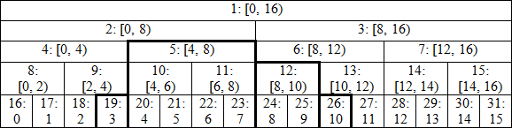
​ 표기하는 방식은 node의 index이다. 해당 세그먼트의 왼쪽 테두리는 포함이고, 오른쪽은 제외한다. 맨 아래 행에는 leaf node인 배열이 있다. 지금은 길이가 2의 거듭 제곱이라고 가정하고 완전 이진트리를 사용한다. 트리를 올라갈 때 인덱스가 있는 노드 쌍을 가져와서 부모의 값을 인덱스 i와 결합한다. 이렇게 하면 구간 [3, 11)에서 합계를 구하라는 쿼리를 받을 때 구간 내의 8개 값 모두가 아니라 19, 5, 12, 26의 값만 합산하면 된다. 구현을 보자.

const int n_LIMIT = 1e5; // limit for array size
int n;			  // array size
int tree[2 * n_LIMIT];

void build()
{
    for (int i = n - 1; i > 0; --i)
    {
        tree[i] = tree[i<<1] + tree[i<<1|1];
    }
}

// set value at position
void modify(int position, int value)
{
    for (tree[position += n] = value; position > 1; position >>= 1)
    {
        tree[position>>1] = t[position] + t[position^1];
    }
}

// sum on interval [left, right)
int query(int left, int right)
{
    int result = 0;
    
    for (left += n, right += n; left < right; left >>=1, right >>= 1)
    {
        if (left & 1)
        {
            result += tree[left++];
        }        
        if (right & 1)
        {
            result += tree[--right];
        }
    }
    
    return result;
}

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; ++i)
    {
        scanf("%d", tree + n + i);
    }
    
    build();
    modify(0, 1);
    print("%d\n", query(3, 11));
    
    return 0;
}

​ 이게 전부이다. 이것이 왜 작동하고 매우 효율적으로 작동하는지 살펴보자.

1. 그림에서 알 수 있듯이 leaf는 n으로 시작하는 인덱스가 있는 연속 노드에 저장되고, 인덱스 i가 있는 요소는 인덱스 i + n이 있는 노드에 해당한다. 따라서 초기 값을 해당 트리에 직접 읽을 수 있다.
2. 쿼리를 수행하기 전에 트리를 구축해야한다. 이는 매우 간단하고 O(n)의 시간 복잡도를 가진다. 부모는 항상 자식보다 인덱스가 적기 때문에 모든 내부 노드를 내림차순으로 처리한다. 비트 연산으로 인해 혼동되는 경우 build()의 코드는 tree[i] = tree[2 * i] + tree[2 * i + 1]과 같다고 생각하면 된다.
3. 요소를 수정하는 것도 매우 간단하며 트리의 높이인 O(log n)에 비례하는 시간 복잡도를 가진다. 주어진 노드의 부모 값만 업데이트 하면 된다. 노드 position의 부모를 찾을 때 왼쪽 자식일 때는 position / 2 또는 position » 1, 오른쪽 자식일 떄는 position ^ 1은 2 * i + 1로 부모의 인덱스를 찾는다.
4. 합계를 찾는 것은 O(log n)의 시간 복잡도를 가진다. 논리를 더 잘 이해하기 위해 [3, 11) 구간으로 예제를 살펴보고 결과가 노드 19, 26, 12, 5의 값으로 정확히 구성되었는지 확인할 수 있었다.

​ 일반적인 아이디어는 다음과 같다. 왼쪽 간격 경계인 left가 홀수이면 (left & 1) left는 부모의 오른쪽 자식이다. 그런 다음 간격은 노드 left를 포함하지만 부모를 포함하지 않는다. 따라서 tree[left]를 더하고, left = (left + 1) / 2 후 left의 부모의 오른쪽으로 이동한다. left가 짝수이면 왼쪽 자식이고 간격에는 부모도 포함된다. 그래서 left = left / 2 로 설정해서 왼쪽으로 이동한다. 오른쪽 경계에도 비슷한 논증이 적용된다. 경계가 만날 때까지 진행하고, 만나면 멈춘다.

​ 재귀도 없고, 간격의 중간을 찾는 것과 같은 추가 계산도 필요하지 않다. 필요한 모든 노드를 통과하기만 하면 되므로 매우 효율적이다.

​

Arbitray sized array (임의 크기의 배열)

​ 지금은 2의 거듭 제곱과 같은 크기의 배열에 대해서만 이야기했으므로 이진 트리는 완벽했다. 다음 사실을 조금 놀라울 수 있다.

The code above works for any size n.

​ 설명은 이전보다 훨씬 더 복잡하므로 이 방법이 주는 이점에 초점을 맞추겠다.

1. 세그먼트 트리는 다른 구현에서 제공하는 것처럼 4 * n이 아닌 정확히 2 * n 메모리를 사용한다.
2. 배열 요소는 인덱스 n부터 시작해 연속적으로 저장된다.
3. 모든 작업은 매우 효율적이고 작성하기 쉽다.

​ 다음 섹션을 건너뛰고 코드가 올바른지 테스트하기만 하면 된다. 설명에 관심이 있는 사람들을 위해 n = 13에 대한 트리가 어떻게 보이는지 다음 그림을 통해 보여주겠다.

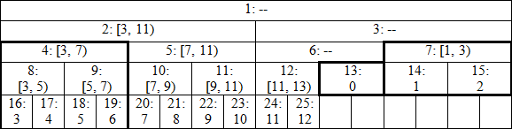
​ 실제로 더 이상 단일 트리가 아니라 완벽한 이진 트리 집합이다. 루트 2와 높이 4, 루트 7과 높이 2, 루트 12와 높이 2, 루트 13과 높이 1이 있다. dashes(?)로 표시된 노드는 쿼리 작업에 사용되지 않으므로 거기에 무엇이 저장되어 있는지는 중요하지 않다. leaf는 높이가 다른 것처럼 보이지만, 노드 13 앞의 트리를 자르고 오른쪽 부분을 왼쪽으로 이동해 해결할 수 있다. 결과 구조가 우리가 수행하는 작업과 관련해 더 큰 완벽한 이진 트리의 일부에 동형으로 보일 수 있다고 믿으며, 이것이 올바른 결과를 얻는 이유이다.

​ 여기서는 공식적인 증명은 신경쓰지 않고, 간격 [0, 7)으로 예제를 살펴보겠다.

left = 13, right = 20, left & 1 => add tree[13]이 있고, 테두리가 left = 7, right = 10으로 변경된다.

left & 1 => add tree[7], 테두리가 left = 4, right = 5.로 변경되고, 노드가 같은 높이에 있다. right & 1 => add tree[4 = –r], 테두리가 left = 2, right = 2로 변경되어 완료된다.

​

Modification on interval, single element access

​ 어떤 사람들은 작업이 반전될 때 어려움을 겪고, 너무 복잡한 것을 발명하기 시작한다. 예를 들면 다음과 같다:

1. 일정 간격으로 모든 요소에 값을 추가한다.
2. 어떤 위치에서 요소를 계산한다.

​ 하지만 이 경우 우리가 해야 할 모든 일은 단지 다음과 같이 modify 및 query 메서드에서 코드를 전환하는 것이다.

void modify(int left, int right, int value)
{
    for (left += n, right += n; left < right; left >>= 1, right >>= 1)
    {
        if (left & 1)
        {
            tree[left++] += value;
        }
        
        if (right & 1)
        {
            tree[--right] += value;
        }
    }
}

int query(int position)
{
    int result = 0;
    
    for (position += n; position > 0; position >>= 1)
    {
        result += tree[position];
    }
    
    return result;
}

​ 수정 후 어느 시점에서 배열의 모든 요소를 검사해야하는 경우 다음 코드를 사용해 모든 수정 사항을 leaf에 푸시할 수 있다. 그 후에 인덱스 n으로 시작하는 요소를 순회 할 수 있다. 이런 식으로 n개의 수정 대신 빌드를 사용하는 것과 유사하게 O(nlog n)에서 O(n)으로 복잡성을 줄인다.

void push()
{
    for (int i = 1; i < n; ++i)
    {
        tree[i<<1] += tree[i];
        tree[i<<1|1] += tree[i];
        tree[i] = 0;
    }
}

​ 그러나 위의 코드는 단일 요소의 수정 순서가 결과에 영향을 미치지 않는 경우에만 작동한다. 예를 들어, assignment는 이 조건을 충족하지 않는다. 자세한 내용은 lazy propagation에 대한 섹션을 참조해라.

​

Non-commutative combiner functions

​ 지금은 가장 간단한 combiner function인 덧셈만 고려했다. 덧셈은 교환법칙이 성립한다. 즉, 피연산자의 순서는 중요하지 않다. a+ b = b + a이다. min 및 max에도 동일하게 적용되므로 +의 모든 발생을 해당 함수 중 하나로 변경해도 잘 작동한다. 그러나 쿼리 결과를 0 대신 무한대로 초기화하는 것을 잊으면 안 된다.

​

​ 그러나 교환법칙이 성립하지 않는 경우가 있다. 다행히 우리의 구현은 이를 쉽게 지원할 수 있다. structure S를 정의하고 이에 대한 기능을 결합한다. 메소드 빌드에서 +를 이 함수로 변경한다. 수정에서 우리는 왼쪽 자식이 인덱스를 가지고 있음을 알고 올바른 자식 순서를 보장해야한다. query에 답할 때 왼쪽 테두리에 해당하는 노드는 왼쪽에서 오른쪽으로 처리되고, 오른쪽 테두리는 오른쪽에서 왼쪽으로 이동한다. 코드에서 다음과 같이 표현할 수 있다.

void modify(int position, const S& value)
{
    for (tree[position += n] = value; position >>= 1; )
    {
        tree[position] = combine(tree[position<<1], tree[position<1|1]);
    }
}
    
S query(int left, int right)
{
	S resultLeft, resultRight;
        
	for (left += n, right += n; left < r; left >>=1, right >>=1)
	{
		if (left & 1)
		{
			resultLeft = combine(resultLeft, tree[left++]);
		}
            
		if (right & 1)
		{
			resultRight = combine(tree[--right], resultRight);
		}
	}
        
	return combine(resultLeft, resultRight);
}