Efficient and easy segment trees - Lazy Propagation
Updated:
Lazy propagation
Lazy propagation(지연 전파)라고 하는 range에 쿼리 및 수정을 모두 수행하는 기술을 설명할 것이다. 먼저 더 많은 변수들이 필요하다:
int h = sizeof(int) * 8 - __builtin_clz(n);
int d[N];
h는 트리의 높이로 n에서 가장 중요한 비트이다. d[i]는 필요할 때 노드 i의 자식으로 전파되는 지연된 작업이다(예제에서 더욱 명확해질 것이다). 리프에 대한 이 정보를 저장할 필요가 없기 때문에 배열의 크기가 N이다. 이로 인해 총 3 * n 메모리 사용량이 발생한다.
이전에는 tree[i]가 세그먼트에 해당하는 값이라고 말할 수 있었다. 지금은 아니다. 먼저 노드 i에서 트리의 루트까지의 경로에서 지연된 모든 작업을 적용해야한다. tree[i]에 이미 d[i]가 포함되어 있으므로 경로가 i로 시작하지 않고, 부모로 시작한다고 가정한다.
범위 [3, 11)를 사용해 첫 번째 예로 돌아가보자. 이제 이 범위 내의 모든 요소를 수정하려고 한다. 이를 위해 노드 19, 5, 12, 26에서 tree[i] 및 d[i]를 수정한다. 나중에 노드 22에서 값을 요청하면 노드 5 밑으로 수정을 전파해야한다. 수정 사항은 트리의 tree[i] 값에도 영향을 미칠 수 있다. 노드 19는 노드 9, 4, 2, 1에 영향을 미치고 노드 5는 2와 1에 영향을 준다. 다음 사실은 작업의 복잡성에 중요하다.
범위 [left, right)에 대한 수정은 border leaves의 부모 (l + n 및 r + n - 1)에서만 tree[i] 값에 영향을 준다 (범위를 구성하는 값은 예외이다 - for 루프에서 액세스한 값).
증명은 간단하다. 왼쪽 경계를 처리 할 때 루프에서 수정하는 노드는 항상 부모의 오른쪽 자식이다. 그런 다음 이전의 모든 수정은 동일한 부모의 왼쪽 자식 하위 트리에서 수행되었다. 그렇지 않으면 두 자식 대신 부모를 처리한다. 이것은 현재 직계 부모도 리프 left + n 의 부모임을 의미한다. 유사한 인수가 오른쪽 테두리에 적용된다.
Increment modifications, queries for maximum
이것은 아마도 가장 간단한 경우이다. 아래 코드는 보편적이지 않고 가장 효율적이지는 않지만 시작하기에 좋다.
void apply(int position, int value)
{
tree[position] += value;
if (position < n)
{
d[p] += value;
}
}
void build(int position)
{
while (position > 1)
{
p>>=1;
tree[position] = max(tree[position<<1], tree[position<<1|1]) + d[p];
}
}
void push(int position)
{
for (int s = h; s > 0; --s)
{
int i = p >> s;
if (d[i] != 0)
{
apply(i<<1, d[i]);
apply(i<<1|1, d[i]);
d[i] = 0;
}
}
}
void inc(int left, int right, int value)
{
left += n;
right += n;
int left0 = left, right0 = right;
for (; left < right; left >>= 1, right >>= 1)
{
if (left & 1)
{
apply(left++, value);
}
if (right & 1)
{
apply(--right, value);
}
}
build(left0);
build(right0 - 1);
}
int query(int left, int right)
{
left += n;
right += n;
push(left);
push(right - 1);
int result = -2e9;
for (; left < right; left >>= 1, right >>= 1)
{
if (left & 1)
{
result = max(result, tree[left++]);
}
if (right & 1)
{
result = max(tree[--right], result);
}
}
return result;
}
한 번에 하나씩 분석해보자. 처음 세 가지는 사용자가 실제로 알 필요가 없는 도우미 메소드이다.
- 이제 모든 내부 노드에 대해 2개의 변수가 있으므로 2가지 모두에 변경 사항을 적용하는 메소드를 작성하는 것이 유용하다. p < n 은 p가 리프인지 아닌지 확인한다. 작업의 중요한 특성은 일정 간격의 모든 요소를 한 값씩 늘리면 최대 값이 같은 값만큼 증가한다는 것이다.
- build 는 주어진 노드의 모든 부모를 업데이트하도록 설계되었다.
- push 는 지정된 노드의 모든 부모에서 루트부터 시작해 트리 아래로 변경 사항을 전파한다. 이 부모는 정확히 이진 표기법에서 position의 prefix 이므로 이진 shift를 사용해 계산한다.
이제 우리는 주요 메소드를 볼 준비가 되었다.
- 위에서 설명한 것처럼 익숙한 루프를 사용해 증가 요청을 처리한 다음 build 를 호출해 필요한 모든 것을 업데이트한다.
- query 에 답하기 위해 이전과 동일한 루프를 사용하지만, 그 전에 모든 변경 사항을 사용할 노드에 푸시해야한다. build 와 마찬가지로 border leaf의 부모에서 변경 사항을 푸시하는 것으로 충분하다.
위의 모든 작업은 O(log n) 시간 복잡도가 걸린다는 것을 쉽게 알 수 있다. 다시 말하지만, 이것은 두 가지 이유 때문에 가장 간단한 경우이다.
- 수정 순서는 결과에 영향을 주지 않는다.
- 노드를 업데이트 할 때 그것이 나타내는 간격의 길이를 알 필요가 없다.
다음 예제에서 이를 고려하는 방법을 보여주겠다.
Assignment modifications, sum queries
다시, helper function부터 시작하자. 이제 우리는 더 많은 것을 가지고 있다.
void calc(int position, int k)
{
if (d[position] == 0)
{
tree[position] = tree[position<<1] + tree[position<<1|1];
}
else
{
tree[position] = d[position] * k;
}
}
void apply(int position, int value, int k)
{
tree[position] = value * k;
if (position < n)
{
d[position] = value;
}
}
이들은 노드 position에서 값을 계산하고 노드에 변경 사항을 적용하는 단순한 O(1) 시간복잡도 함수이다. 그러나 설명할 두 가지가 있다.
- 수정에 사용하지 않는 값이 있다고 가정하자. 우리의 경우에는 0이다. 그러한 값이 없는 경우 - 추가 부울 배열을 만들고 d[position] == 0 을 확인하는 대신 부울 배열을 참조한다.
- 이제 노드 position에 해당하는 간격의 길이를 나타내는 추가 매개 변수 k가 있다. 이 의미를 보존하기 위해 코드에서 이 이름을 일관되게 사용할 것이다. 분명히 이 매개 변수없이 합계를 계산하는 것은 불가능하다. 별도의 배열에 있는 모든 노드에 대해 이 값을 미리 계산하거나 노드 인덱스에서 즉석에서 계산하는 경우 이 매개 변수 전달을 피할 수 있지만, 추가 메모리나 계산을 사용하지 않는 방법을 보여주겠다.
다음으로 build 및 push 메소드를 업데이트해야 한다. 두 가지 버전이 있다. 하나는 O(n)에서 전체 트리를 처리하는 이전에 소개한 것, 다른 하나는 O(log n)에서 한 잎의 부모만 처리하는 마지막 예에서 가져온 것이다. 이 기능을 하나의 방법으로 쉽게 결합하고 더 많은 것을 얻을 수 있다.
void build(int left, int right)
{
int k = 2;
for (left += n, right += n - 1; left > 1; k <<= 1)
{
left >>= 1;
right >>= 1;
for (int i = right; i >= left; --i)
{
calc(i, k);
}
}
}
void push(int left, int right)
{
int s = h, k = 1 << (h - 1);
for (left += n, right += n - 1; s > 0; --s, k >>= 1)
{
for (int i = l >> s; i <= r >> s; ++i)
{
if (d[i] != 0)
{
apply(i<<1, d[i], k);
apply(i<<1|1, d[i], k);
d[i] = 0;
}
}
}
| 이 두 방법 모두 O(log (n) + | right - left | ) 시간의 모든 간격에서 작동한다. 트리에서 일부 간격을 변환하려면 다음과 같은 코드를 작성할 수 있다. |
push(left, right);
. . . // do anything we want with elements in interval [left, right)
build(left, right);
그들이 어떻게 작동하는지 설명하자. 먼저 부모를 올바르게 계산하기 위해 right += n - 1을 수행해 구간을 닫힘으로 변경한다. 레벨별로 트리 레벨을 처리하기 때문에 현재 간격 레벨을 유지하기가 쉽지 않다. 이 간격 레벨은 항상 2의 거듭 제곱이다. build 는 아래에서 위로 이동하므로 k를 2로 초기화하고(리프에 대해 아무것도 계산하지 않고, 직계 부모로 시작하기 때문에 1이 아니다), 각 레벨에서 두 배로 늘린다. push 는 위에서 아래로 이동하므로 k의 초기 값은 여기에서 나무의 높이에 따라 다르며 각 레벨에서 2로 나뉜다.
주요 메소드는 마지막 예제에서 많이 변경되지 않지만 modify에는 2가지 사항이 있다.
- 수정 순서가 중요하기 때문에 루트에서 업데이트 할 모든 노드까지의 경로에 이전 변경 사항이 없는지 확인해야한다. query에서 했던 것처럼 push를 먼저 호출하면 된다.
- k의 값을 유지해야한다.
void modify(int left, int right, int value)
{
if (value == 0)
return;
push(left, left + 1);
push(right - 1, right);
int left0 = left, right0 = right, k = 1;
for (left += n, right += n; left < right; left >>= 1, right >>= 1, k <<= 1)
{
if (left & 1)
{
apply(left++, value, k);
apply(--right, value, k);
}
}
build(left0, left0 + 1);
build(right0 - 1, right0);
}
int query(int left, int right)
{
push(left, left + 1);
push(right - 1, r);
int result = 0;
for (left += n, right += n; left < right; left >>= 1, right >>= 1)
{
if (left & 1)
{
result += tree[left++];
}
if (right & 1)
{
result += tree[--right];
}
}
return result;
}
거의 동일한 노드에 대해 3개의 전달된 수정 작업을 수행하는 것을 알 수 있다. 1은 push 트리 아래로, 2는 트리 위로 이동한다. 마지막 패스를 제거하고 필요한 경우에만 새 값을 계산할 수 있지만 코드는 더 복잡해진다.
void modify(int left, int right, int value)
{
if (value == 0)
return;
push(left, left + 1);
push(right - 1, right);
bool cLeft = false, cRight = false;
int k = 1;
for (left += n, right += n; left < right; left >>= 1, right >>= 1, k <<= 1)
{
if (cLeft)
{
calc(left - 1, k);
}
if (cRight)
{
calc(right, k);
}
if (left & 1)
{
apply(left++, value, k), cLeft = true;
apply(--right, value, k), cRight = true;
}
}
for (--left; right > 0; left >>= 1, right >>= 1, k <<= 1)
{
if (cLeft)
{
calc(left, k);
}
if (cRight && (!cLeft || left != right))
{
calc(right, k);
}
}
}
부울 플래그는 왼쪽과 오른쪽을 이미 변경했는지 여부를 나타낸다. 예를 살펴보자:
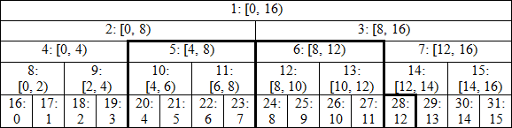
간격 [4,13)에서 modify를 호출한다
- left = 20, right = 29, apply(28)을 호출한다.
- left = 10, right = 14, calc(14)를 호출한다. 현재 간격의 오른쪽에 있는 첫 번째 노드는 정확히 마지막으로 수정된 노드의 부모이다.
- left = 5, right = 7, calc(7)을 호출하고, apply(5)와 apply(6)을 호출한다.
- left = 3, right = 3, 첫 번째 루프가 끝났다.
이제 노드 2, 3, 1에서 새 값을 계산해야 하기 때문에 –left를 수행하는 지점을 볼 수 있다. 첫 번째 이후 left = 1, right = 1을 얻을 수 있기 때문에 끝 조건은 r > 0이다. 루프이므로 루트를 업데이트해야 하지만 –left 결과는 left = 0이다.
이전 구현과 비교해 불필요한 호출 calc(10), calc(5), calc(1)에 대한 중복 호출을 방지한다.
Leave a comment